Богданов К.Ю.

kbogdanov1@yandex.ru

 

см. другие сайты и вебстраницы автора:

Что такое финансовый кризис?

Что такое жизнь?

Почему у блика на фото несколько лучей?

Антибликовые очки и ЖК-дисплей

Что заставляет женщин вилять бёдрами?

Почему кучевые облака плоские снизу?

Далеко ли мы от Тадж-Махала?

Загадки одномерного бильярда

Электростатика заряженных бусинок

Физика внутри нас

Популярно обо всём

Почему, что и как?

Что могут нанотехнологии?

 

 

Ночным поездом по коническим сечениям

с транспортиром, но без ноутбука

 

Представьте, что ночью выглянули из окна движущегося поезда и вдали увидели одинокий огонёк. Проносятся мимо километровые столбы, и изменяется угол b, под которым этот огонёк виден из окна вагона. Можно ли измеряя только направление на огонёк и читая надписи на километровых столбах, выяснить, по какой кривой движется поезд? Можно ли, например, отличить движение по прямой от движения по гиперболе, окружности или эллипсу?

Такой или почти такой вопрос задал мне один из школьников на уроке астрономии. Конечно, после достаточно сложного (численного) анализа изменений b при движении поезда можно определить его траекторию. Но можно ли это сделать без ноутбука в багаже? Другими словами, как, взглянув на изменение b, сделать вывод о траектории движения поезда? Я постарался ответить на этот вопрос, но не уверен, что прав.

Сначала условимся, как мы измеряем угол b, под которым виден этот «огонёк» из окна поезда (рис.1). За угол b примем угол между нормалью к траектории и направлением на огонёк. Пусть при этом угол b будет положительным, если огонёк находится впереди по движению поезда. Тогда на рис.1 показана ситуация, когда b<0.

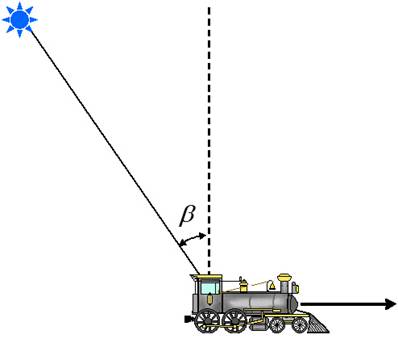
Рисунок 1. Измерение угла b, под которым виден «огонёк» по отношению к нормали (пунктир) к траектории движения поезда. Вид сверху.

 

Поезд на прямой. Если траектория движения поезда прямая, то угол b будет изменяться так, как это показано на рис.2.

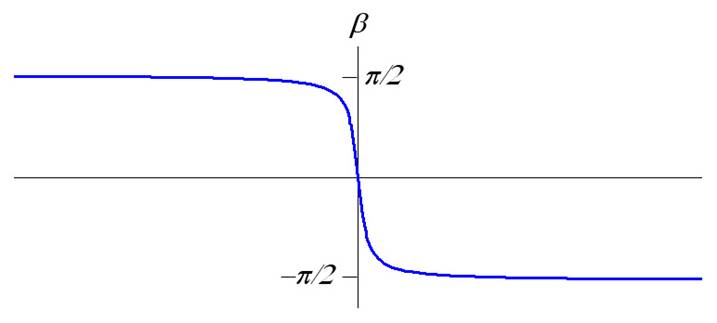
Рисунок 2. Изменение угла b, под которым виден «огонёк» при движении поезда по отрезку прямой.

 

Из рис.2 следует, что при движении вагона по прямой угол b монотонно уменьшается. При  этом количество экстремумов (Э) этой кривой равно нулю и кривая пересекает ось абсцисс только один раз (N0=1). Таким образом, зависимость b при движении вагона по прямой можно охарактеризовать двумя параметрами (Э=0, N0=1).

 

Поезд на гиперболе. Пусть теперь поезд движется по гиперболе, постепенно поворачивая на 90°. Моделирование на компьютере позволяет для такого движения построить зависимость b от пройденного пути при любых положениях «огонька» относительно фокуса гиперболы (см. рис. 3, а, б, в).

 

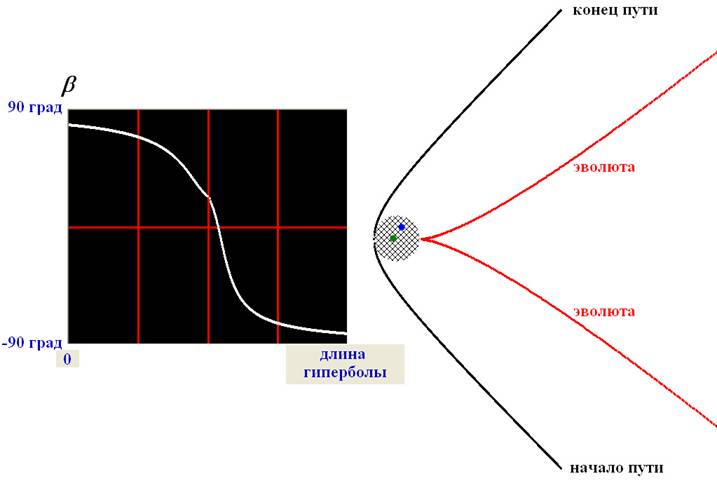
Рисунок 3а. Слева - изменение угла b, под которым виден «огонёк». Справа – часть гиперболы, по которой едет поезд с фокусом, обозначенным зелёным кружком; синим кружком обозначено положение «огонька»; красные кривые – эволюта гиперболы; заштрихована область вокруг фокуса, где кривая изменений b не имеет экстремумов.

 

 

 

 

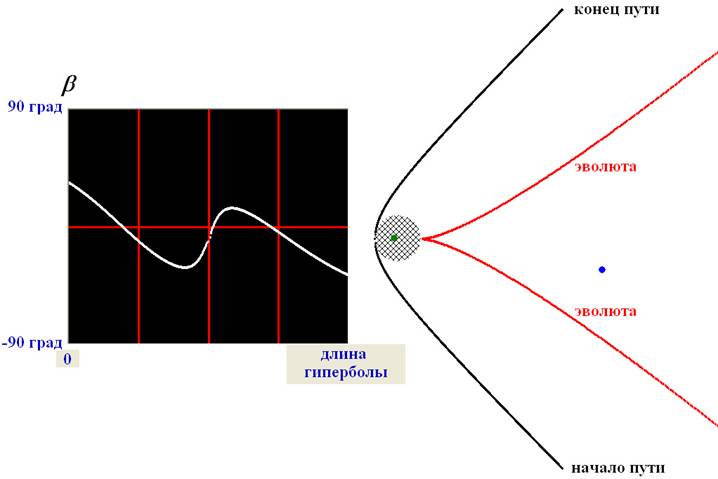
Рисунок 3б. Слева - изменение угла b, под которым виден «огонёк». Справа – часть гиперболы, по которой едет поезд с фокусом, обозначенным зелёным кружком; синим кружком обозначено положение «огонька»; красные кривые – эволюта гиперболы; заштрихована область вокруг фокуса, где кривая изменений b не имеет экстремумов.

 

 

 

 

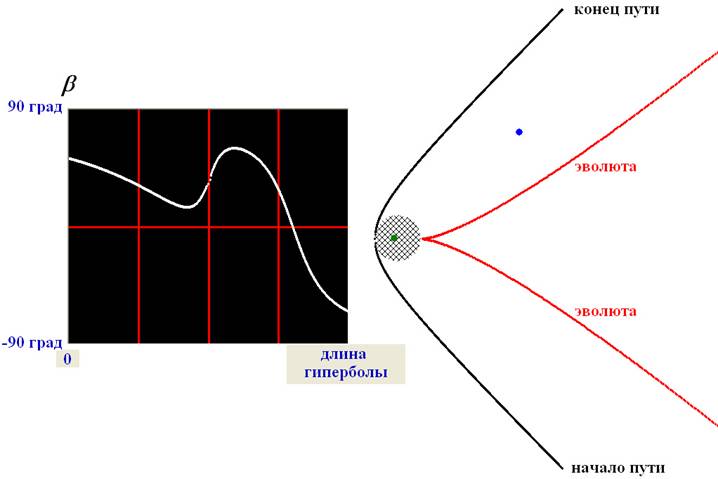
Рисунок 3в. Слева - изменение угла b, под которым виден «огонёк». Справа – часть гиперболы, по которой едет поезд с фокусом, обозначенным зелёным кружком; синим кружком обозначено положение «огонька»; красные кривые – эволюта гиперболы; заштрихована область вокруг фокуса, где кривая изменений b не имеет экстремумов.

 

Оказывается, при движении по гиперболе зависимость b от пройденного пути имеет либо 2 экстремума (Э=2 на рис. 3, б и в), либо ни одного (Э=0 на рис. 3, а). Кривая с Э=0 и N0=1 соответствует тем случаям, когда «огонёк» расположен в очень небольшой области вблизи фокуса гиперболы (заштрихована на рис. 3, а).  Если «огонёк» находится в остальных местах между ветвями гиперболы, то кривая изменения b имеет два экстремума (Э=2).

Зависимости b от пройденного пути пересекает изолинию в одной (N0=1) точке, если «огонёк» находится слева от эволюты гиперболы, которая обозначена красной кривой на рисунках 3, а, б и в. Если же огонёк находится справа от эволюты (рис. 3, в), то зависимость b от пройденного пути пересекает изолинию в трёх (N0=3) точках.

 

Поезд на параболе. При движении по параболе зависимость b от пройденного пути очень похожа на ту, что характерна для движения по гиперболе. Эта зависимость имеет либо 2 экстремума, либо ни одного. При этом кривая с Э=0 и N0=1 соответствует тем случаям, когда «огонёк» расположен в небольшой области вблизи фокуса параболы, а в остальных местах кривая характеризуется Э=2, и при этом N0=1 или N0=3 в зависимости от того огонёк находится слева или справа от эволюты параболы.

 

Поезд на окружности. Известно, что вокруг многих городов существуют кольцевые железные дороги. На рис.4 показано, как изменяется угол b, под которым виден «огонёк», при движении по окружности.

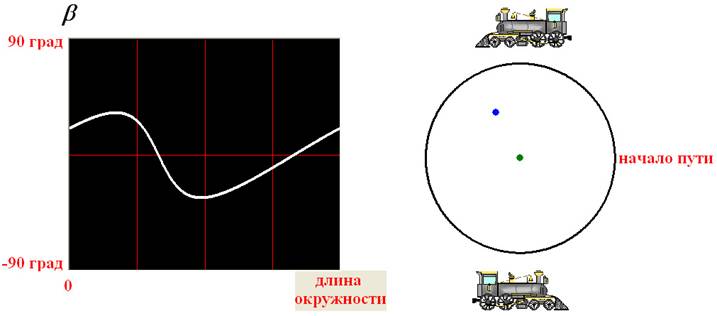
Рисунок 4. Слева - изменение угла b, под которым виден «огонёк». Справа – окружность, по которой едет поезд с центром, обозначенным зелёным кружком; синим кружком обозначено положение «огонька».

 

Видно, что зависимость b от положения на окружности имеет два экстремума (Э=2) и два раза пересекает изолинию (N0=2). Амплитуда экстремумов растёт с удалением от центра окружности, но их число и число пересечений изолинии не изменяется.

 

Поезд на эллипсе. При движении по эллипсу изменение b оказывается более сложным, чем по окружности (рис.5, а, б, в).

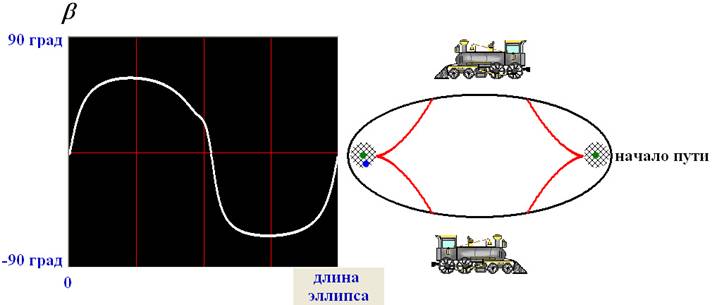
Рисунок 5а. Слева - изменение угла b, под которым виден «огонёк». Справа – эллипс, по которому едет поезд с фокусами, обозначенными зелёными кружками; синим кружком обозначено положение «огонька»; красные кривые – эволюты эллипса, лежащие внутри него; заштрихованные кружки вокруг фокусов эллипса приблизительно обозначают области, где кривая изменений b имеет два экстремума.  

 

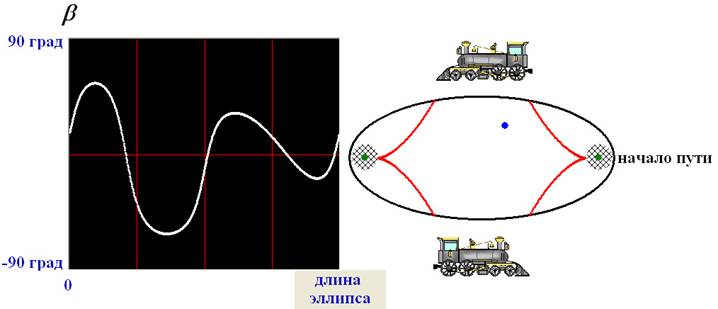
Рисунок 5б. Слева - изменение угла b, под которым виден «огонёк». Справа – эллипс, по которому едет поезд с фокусами, обозначенными зелёными кружками; синим кружком обозначено положение «огонька»; красные кривые – эволюты эллипса, лежащие внутри него; заштрихованные кружки вокруг фокусов эллипса приблизительно обозначают области, где кривая изменений b имеет два экстремума. 

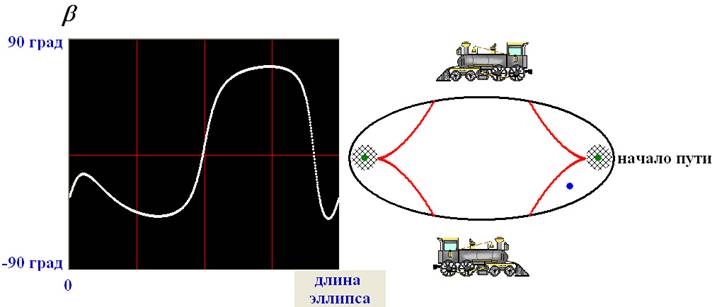
Рисунок 5в. Слева - изменение угла b, под которым виден «огонёк». Справа – эллипс, по которому едет поезд с фокусами, обозначенными зелёными кружками; синим кружком обозначено положение «огонька»; красные кривые – эволюты эллипса, лежащие внутри него; заштрихованные кружки вокруг фокусов эллипса приблизительно обозначают области, где кривая изменений b имеет два экстремума. 

 

Как следует из рис.5, при движении по эллипсу зависимость b от пройденного пути имеет либо 4 экстремума (Э=4 на рис. 5, б и в), либо два (Э=2 на рис. 5, а). Кривая с Э=2 и N0=2 соответствует тем случаям, когда «огонёк» расположен в очень небольшой области вблизи фокусов эллипса (заштрихована на рис. 5, а).  Если «огонёк» находится в остальных местах, то кривая характеризуется Э=4 и при этом N0=2 (рис. 5, в) или N0=4 (рис. 5, б). Легко догадаться, что N0=4 для тех «огоньков», которые лежат между ветвями эволют, а N0=2 соответствуют огонькам, расположенным снаружи ветвей эволют эллипса.

 

Подводим итоги. Таким образом, характеристики зависимости угла b, под которым виден «огонёк»,  от пройденного пути могут быть сведены в следующую таблицу  

Таблица 1. Характеристики зависимости b для разных типов конического сечения

 

Как следует из таблицы 1, считая число экстремумов и пересечений изолиний зависимости b от пройденного пути, вполне можно различить между собой прямую и гиперболу, окружность или эллипс. Что касается, гиперболы и параболы, то такой простой анализ зависимости b не даёт возможности прийти к какому-либо заключению.

Остаётся непонятным, от чего зависят размеры и форма областей вблизи фокусов, где число экстремумов (Э) зависимости b от пройденного пути уменьшается на 2.